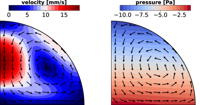
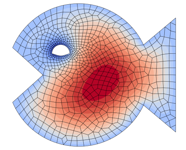
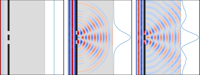
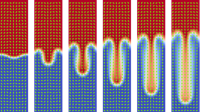
Information
pyoomph is an
object-
oriented
multi-
physics finite element framework for
Python. It is mainly a custom high level frontend for the prime functionalities of the powerful C++ library
oomph-lib. While pyoomph does not support the entire plethora of features provided by oomph-lib, pyoomph follows a complementary approach, allowing for rapid development and e.g. automatic nondimensionalization and advanced stability analysis beyond oomph-lib's native capabilities.
Tutorial
The
full tutorial can be found here, but below please find some examples to start with:
Features
- • Temporal ordinary differential equations •
- • Spatial boundary value problems •
- • Spatio-temporal problems •
- • Moving mesh (ALE) problems •
- • Automatic mesh reconstruction •
- • Spatial & temporal adaptivity •
- • Mixed elements •
- • Additional fields at interfaces •
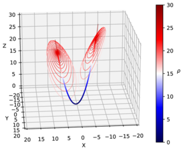
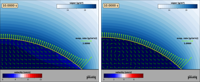
- • Stability analysis & bifurcation tracking •
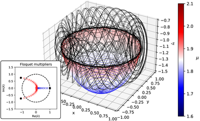
- • Periodic orbits & Floquet multipliers •
- • Linear response to periodic driving •
- • Azimuthal stability analysis •
- • Follow eigenbranches •
- • Nonlinear elasticity •
- • Fully symbolically derived Jacobian/Hessian •
- • Automatic non-dimensionalization •
- • Continuous and Discontinuous Galerkin Methods •
- • Multi-Domain and Multi-Physics •
- • Coordinate-system-agnostic formulation of equations •
- • Constraints via Lagrange multipliers •
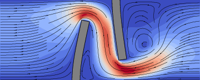
- • Free surface dynamics with Marangoni flow •
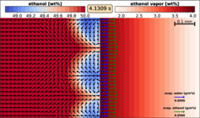
- • Multi-component flow with mass transfer •
- • Vapor-liquid equilibria by group contribution models •
- • Surfactants with versatile isotherms •
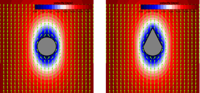
- • Contact line dynamics •
- • Cartesian normal model analysis •
- • Coupling simulations via a preCICE adapter •
- • Fluid-structure interaction •
How it works
Formulating custom equations, meshes, problems and materials properties is directly done in Python. Subsequently, once the problem is assembled, the monolithic Jacobian matrix is symbolically derived. To speed up the assembly process, C code to fill the residuals and the Jacobian matrix is automatically generated, compiled and loaded back to the running program. For the code generation, pyoomph makes use of
GiNaC and
CLN. Besides symbolically derived Jacobian matrices, also parameter derivatives and Hessians, even including the complicated derivatives with respect to the moving mesh coordinates on a symbolical level, are transferred to performant C code. The generated code is compiled and linked back to the running python script, either with the
TinyC compiler (invoked by
tccbox) or, when installed, with a more performant alternative like
gcc,
LLVM/clang or
MSBuild. Thereby, pyoomph is on par with hand-written implementations in a compiled programming language, yet with the ease of Python as scripting language. This approach allows for rapid development of complicated multi-physics and multi-domain problems, including physical dimensions (units) and realistic material properties, varying e.g. with the temperature or the composition.
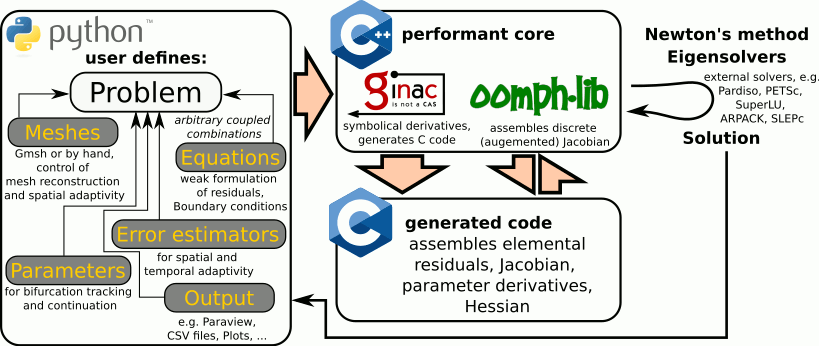
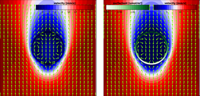
[From our paper Christian Diddens and Duarte Rocha, Bifurcation tracking on moving meshes and with consideration of azimuthal symmetry breaking instabilities, J. Comput. Phys. 518, 113306, (2024).]